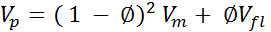Notes on GeoSyn fluid replacement
Introduction
GeoSyn uses the Biot-Gassman fluid substitution method.
There are other approaches to fluid substitution (empirical and heuristic) which avoid the porous frame calculations but often do not yield reliable results. GeoSyn provides some empirical Vp information (Wyllie’s time average, Average Velocity and Raymers equation) as a check for consistency between the modelled log data and the in-situ rock parameters. In general, and in particular for Wyllie’s equation, these empirical relationships fall down when substituting gas for water and cannot be used reliably for fluid substitution.
The following overview is based largely on the bible of the field "The Rock Physics Handbook."
Some basic equations
The mechanics of fluid substitution on the density and shear logs is simple. For the density log, fluid substitution can be written:
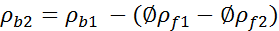 (1)
(1)
where 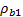 is the initial rock bulk density,
is the initial rock bulk density, 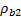 is the bulk rock density after fluid substitution,
is the bulk rock density after fluid substitution,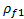 is the initial fluid density,
is the initial fluid density, 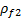 is the density of the substituting fluid, and φ is the porosity. The substituted rock density
is the density of the substituting fluid, and φ is the porosity. The substituted rock density 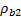 is simply the fractional difference attributable to the fluid change in the pore space.
is simply the fractional difference attributable to the fluid change in the pore space.
Given the fact that in Biot-Gassmann’s model the shear modulus μ is independent of the pore fill, the substituted Vs depends only on the change in density:
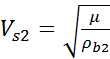 (2)
(2)
This means, of course, that substitution of hydrocarbon for water will result in a lowering of bulk density and an increase in Vs.
Calculating the fluid substitution effect on the compressional wave velocity 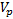 , as measured by the sonic log, is not so straightforward because it depends not only on the substituted density and the shear modulus, but also on the saturated bulk modulus Ksat:
, as measured by the sonic log, is not so straightforward because it depends not only on the substituted density and the shear modulus, but also on the saturated bulk modulus Ksat:
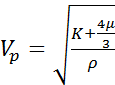 (3)
(3)
In turn, the bulk modulus of the new rock 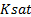 requires knowledge of the mineral modulus
requires knowledge of the mineral modulus 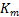 , the fluid modulus
, the fluid modulus 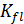 and the bulk modulus of the unsaturated rock
and the bulk modulus of the unsaturated rock 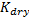 (Mavko and Mukerji, 1995; Avseth et al., 2005):
(Mavko and Mukerji, 1995; Avseth et al., 2005):
The Biot-Gassman equations
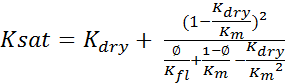 (4)
(4)
Solving for 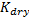
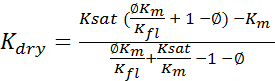 (5)
(5)
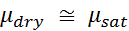
The shear modulus is the same dry or saturated.
Where
 = shear wave velocity
= shear wave velocity
 =compressional wave velocity
=compressional wave velocity
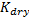 =effective bulk modulus of dry rock
=effective bulk modulus of dry rock
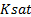 =effective bulk modulus of the rock with pore fluid
=effective bulk modulus of the rock with pore fluid
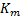 =bulk modulus of mineral material making up rock
=bulk modulus of mineral material making up rock
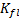 =effective bulk modulus of pore fluid
=effective bulk modulus of pore fluid
 =porosity (fractional)
=porosity (fractional)
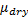 =effective shear modulus of dry rock
=effective shear modulus of dry rock
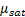 =effective shear modulus of rock with pore fluid
=effective shear modulus of rock with pore fluid
Performing the fluid substitution
In plain terms the Biot-Gassman relationship allows one to calculate the saturated bulk modulus and resultant Vp (equation 3) from a combination of the dry bulk modulus 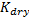 , the fluid bulk modulus
, the fluid bulk modulus 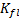 and the mineral bulk modulus
and the mineral bulk modulus 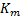 .
.
Modeling the changes from one fluid type to another requires that the effects of the starting fluid first be removed prior to modeling the new fluid. i.e. calculate 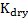 . In practice, the rock is drained of its initial pore fluid, and the moduli (bulk and shear) and bulk density of the porous frame are calculated. Once the porous frame properties are properly determined, the rock is saturated with the new pore fluid, and the new effective bulk modulus and density are calculated.
. In practice, the rock is drained of its initial pore fluid, and the moduli (bulk and shear) and bulk density of the porous frame are calculated. Once the porous frame properties are properly determined, the rock is saturated with the new pore fluid, and the new effective bulk modulus and density are calculated.
A direct result of Gassmann's equations is that the shear modulus for an isotropic material is independent of pore fluid, and therefore remains constant during the fluid substitution process. In the case of disconnected or crack like pores, however, this assumption may be violated. Once the values for the new effective bulk modulus and bulk density are calculated, it is possible to calculate the compressional and shear velocities for the new fluid conditions.
A two-step calculation is required. In-situ saturation to dry saturation followed by dry saturation to new fluid saturation.
1. Calculate the dry bulk modulus using the in-situ saturated bulk modulus 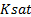 and in-situ fluid modulus
and in-situ fluid modulus 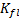 .
. 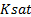 is calculated using equation 3, which is where the original log data
is calculated using equation 3, which is where the original log data 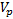 is used.
is used.
2. Calculate the new saturated bulk modulus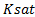 using the dry bulk modulus
using the dry bulk modulus 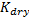 and a new fluid modulus
and a new fluid modulus 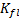 reflecting the changes in gas/water saturation. With the new
reflecting the changes in gas/water saturation. With the new 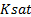 and using equation 3 a new
and using equation 3 a new 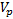 can be calculated.
can be calculated.
What can a GeoSyn user take from this?
The in-situ reservoir parameters for matrix bulk and shear modulus and density must be correct for the log section being analyzed.
For example you could incorrectly describe an extremely high modulus matrix then apply it to a log section of very slow velocity. In reality such a rock should be quite fast. The equations will fail.
GeoSyn provides several empirical relationships to give users a ball park theoretical Vp based on the reservoir parameters. The Vp calculated from one or all of these equations should roughly match the Vp of the log data or something is wrong and the Biot-Gassman equations will not work properly. Note that these empirical relationships are not reliable when gas is the pore fluid. If they were reliable then the trouble and trickiness of using the Biot-Gassman equations would be unnecessary.
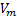 is calculated using equation 3
is calculated using equation 3
Wyllies time average equation
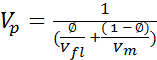
Velocity average equation
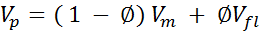
Raymers equation